

A distância entre um objeto e a imagem que um espelho esférico lhe conjuga mede 15 cm. Sendo ambos reais, com o objeto apresentando altura o dobro da imagem, determine a natureza do espelho e a sua distância focal.
(A) Espelho convexo e distância focal de 10,0 cm.
(B) Espelho côncavo e distância focal de 3,3 cm.
(C) Espelho convexo e distância focal de 3,3 cm.
(D) Espelho côncavo e distância focal de 10,0 cm.
(E) Espelho côncavo e distância focal de 1,5 cm.
Resolução:
Sendo uma imagem REAL, podemos afirmar que trata-se de um espelho côncavo, pois o espelho convexo não conjuga imagens reais.
Do enunciado, temos:
\(H_{objeto} = 2.H_{imagem} \)
logo
\(d_{objeto} = 2.d_{imagem} \)
O único caso onde \(H_{objeto} > H_{imagem} \) é quando o objeto está posicionado além do centro de curvatura do espelho e a imagem estará conjugada entre o centro e o foco.
Observe a imagem a seguir.
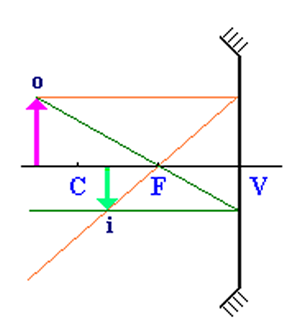
O enunciado afirma que a distância entre a posição do objeto e a posição da imagem é igual a 15cm. Matematicamente podemos escrever que
\(d_{objeto} - d_{imagem} =15cm \)
Podemos montar um sistema de equações:
\[ \left\{\begin{matrix} d_{objeto} - d_{imagem} =15 &\textrm{(equação 1)} \\ d_{objeto} = 2d_{imagem}&\textrm{(equação 2)} \\ \end{matrix}\right. \] Substituindo a equação 2 na equação 1, teremos: \[ \begin{aligned} 2d_{imagem} - d_{imagem} =15 \rightarrow d_{imagem}=15\\ \end{aligned} \]
Chegamos aos valores
\[ \begin{aligned} d_{imagem}=15\\ d_{objeto}=30\\ \end{aligned} \]que poderemos aplicar na equação de Gauss para espelhos esféricos delgados \[ \begin{aligned} \frac{1}{d_{focal}}=\frac{1}{d_{imagem}}+\frac{1}{d_{objeto}}\\ \frac{1}{d_{focal}}=\frac{1}{15}+\frac{1}{30}\\ \frac{1}{d_{focal}}=\frac{2+1}{30}\\ \frac{1}{d_{focal}}=\frac{3}{30}\\ \frac{30}{3}=d_{focal}\\ d_{focal} = 10cm \end{aligned} \]
Alternativa (D)