Coeficiente de dilatação superficial

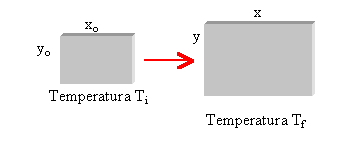
Uma placa retangular é feita de um material cujo coeficiente de dilatação linear é . Os lados da placa medem  e  à temperatura . Aumentando-se a temperatura para , os lados passam a medir x e y. Nesse caso, a variação de temperatura é .

Podemos então escrever:

Multiplicando as equações membro a membro, temos:

O produto  representa a área da placa à temperatura  e o produto xy representa a área à temperatura :

 e

Temos, então:

Vamos analisar a potência :

Sabemos que o coeficiente de dilatação linear  tem ordem de grandeza . Na maioria dos casos reais, a ordem de grandeza de  é, no máximo, . Teremos, então, as ordens de grandeza:

A parcela  é desprezível em face de . Por isso, não vamos considera-la:

Temos então:

A constante é chamada de coeficiente de dilatação superficial do material e é representada pela letra .

Adaptado de “Física”  de Chiquetto & Parada