Densidade
Definição: Densidade é a razão entre a massa de um objeto e seu volume. Em outras palavras, é a quantidade de massa por unidade de volume.
Fórmula: \(\rho = \frac{m}{V}\), onde \(\rho\) (rho) representa a densidade, \(m\) é a massa e \(V\) é o volume.
Unidades Comuns: No Sistema Internacional (SI), a densidade é medida em quilogramas por metro cúbico (kg/m³). Outras unidades comuns incluem gramas por centímetro cúbico (g/cm³).
Aplicações: A densidade é usada para descrever a "compactação" de uma substância, independentemente de ser sólida, líquida ou gasosa. Por exemplo, a densidade da água é aproximadamente 1 g/cm³.
Massa Específica
Definição: Massa específica é a razão entre a massa de uma substância e o volume ocupado por essa substância. É similar à densidade, mas normalmente é usada para descrever líquidos e substâncias em contextos específicos.
Fórmula: \(\mu = \frac{m}{V}\), onde \(\mu\) representa a massa específica, \(m\) é a massa e \(V\) é o volume.
Unidades Comuns: Semelhante à densidade, a massa específica é medida em kg/m³ no SI e g/cm³ em outras situações.
Aplicações: Massa específica é frequentemente usada em química e engenharia para descrever líquidos e materiais, especialmente em contextos onde a densidade pode variar com a temperatura e a pressão.
Diferenças
Terminologia e Contexto: Embora densidade e massa específica sejam matematicamente equivalentes, o termo "densidade" é mais frequentemente usado em contextos gerais e para sólidos, enquanto "massa específica" é mais utilizada em contextos de engenharia e química para líquidos.
Uso Prático: A densidade é uma propriedade intensiva que independe da quantidade de material, enquanto a massa específica é frequentemente usada para descrever materiais em condições específicas, como temperatura e pressão constantes.
Exemplo
Água:
A massa específica (\(\mu\)) de uma substância é a razão entre a massa (m) de uma quantidade da substância e o volume (V) correspondente:
\(\mu = \frac{m}{V}\)
Uma unidade muito usual para a massa específica é o g/cm³, mas no SI a unidade é o kg/m³. A relação entre elas é a seguinte:
\(\frac{1 \, \text{g}}{\text{cm}^3} = \frac{10^{-3} \, \text{kg}}{10^{-6} \, \text{m}^3} = 10^3 \, \text{kg/m}^3\)
Assim, para transformar uma massa específica de g/cm³ para kg/m³, devemos multiplicá-la por 1.000. Na tabela a seguir estão relacionadas as massas específicas de algumas substâncias.
| Substância | \(\mu = \frac{g}{cm^3}\) | \(\mu = \frac{kg}{m^3}\) |
|---|---|---|
| Água | 1,0 | 1.000 |
| Gelo | 0,92 | 920 |
| Álcool | 0,79 | 790 |
| Ferro | 7,8 | 7.800 |
| Chumbo | 11,2 | 11.200 |
| Mercúrio | 13,6 | 13.600 |
É comum encontrarmos o termo densidade (d) em lugar de massa específica (m). Usa-se "densidade" para representar a razão entre a massa e o volume de objetos sólidos (ocos ou maciços), e "massa específica" para líquidos e substâncias.
Exemplo: São misturados volumes iguais de dois líquidos com massas específicas de \(0,50 \, \text{g/cm}^3\) e \(0,90 \, \text{g/cm}^3\). Determine a massa específica da mistura.
Resolução: Sendo os volumes iguais, temos \(V_1 = V_2 = V\). Portanto, o volume da mistura é \(2V\). Por outro lado, podemos dizer que a massa da mistura é igual à soma das massas dos dois líquidos.
Da relação \(\mu = \frac{m}{V}\), temos \(m = \mu V\):
\(\mu_{\text{mistura}} = \frac{\mu_1 + \mu_2}{2} \)
\(\mu_{\text{mistura}} = \frac{0,50 + 0,90}{2} \)
\(\mu_{\text{mistura}} = 0,70 \, \text{g/cm}^3\)
Exercícios:
1. Determine a massa de um bloco de chumbo que tem arestas de 10 cm.
2. A caixa mostrada na figura é oca e suas paredes apresentam 2 cm de espessura.
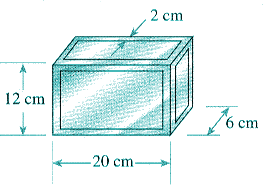
Sabendo-se que ela possui 2,0 kg de massa, determine:
a) a densidade da caixa;
b) a massa específica da substância usada na confecção da caixa.
3. Uma esfera oca, de 1.200 g de massa, possui raio externo de 10 cm e raio interno de 9,0 cm. Sabendo que o volume de uma esfera é dado por \(V = \frac{4}{3}\pi r^3\), determine:
a) a densidade da esfera;
b) a massa específica do material de que é feita a esfera.
(Use \(\pi \approx 3,14\)).
4. Misturam-se massas iguais de dois líquidos de massas específicas 0,40 \(\text{g/cm}^3\) e 1,0 \(\text{g/cm}^3\).
Determine a massa específica da mistura.
Resoluções
Problema 1
A fórmula para o volume de um cubo é \(V = a^3\), onde \(a\) é a aresta do cubo.
\( V = 10^3 = 1000 \, \text{cm}^3 \)
A densidade do chumbo (\(\rho\)) é aproximadamente
\(11,34 \, \text{g/cm}^3\).
A massa (\(m\)) é dada por
\(m = \rho \times V\)
\(m = 11,34 \times 1000 \)
\(m = 11340 \, \text{g} \)
\(m = 11,34 \, \text{kg} \)
Problema 2
a) A densidade (\(\rho\)) é dada por \(\rho = \frac{m}{V}\).
Para calcular o volume, precisamos subtrair o volume interno do volume externo.
Volume externo (\(V_{\text{ext}}\)):
\( V_{\text{ext}} = 20 \times 12 \times 6 \)
\( V_{\text{ext}} = 1440 \, \text{cm}^3 \)
Volume interno (\(V_{\text{int}}\)):
\(V_{\text{int}} = (20 - 4) \times (12 - 4) \times (6 - 4) \)
\(V_{\text{int}} = 16 \times 8 \times 2 \)
\( V_{\text{int}} = 256 \, \text{cm}^3 \)
Volume total da caixa (\(V\)):
\( V = V_{\text{ext}} - V_{\text{int}} \)
\( V = 1440 - 256 \)
\( V = 1184 \, \text{cm}^3 \)
Densidade da caixa:
\( \rho = \frac{2000}{1184} \)
\( \rho \approx 1,69 \, \text{g/cm}^3 \)
b)
A massa específica da substância usada na confecção da caixa é a mesma que a densidade da caixa:
\( \mu \approx 1,69 \, \text{g/cm}^3 \)
Problema 3
Volume externo (\(V_{\text{ext}}\)):
\( V_{\text{ext}} = \frac{4}{3} \pi (10)^3 \)
\( V_{\text{ext}} = \frac{4}{3} \times 3,14 \times 1000 \)
\( V_{\text{ext}} \approx 4186,67 \, \text{cm}^3 \)
Volume interno (\(V_{\text{int}}\)):
\( V_{\text{int}} = \frac{4}{3} \pi (9)^3 \)
\( V_{\text{int}} = \frac{4}{3} \times 3,14 \times 729 \)
\( V_{\text{int}} \approx 3053,63 \, \text{cm}^3 \)
Volume da esfera oca (\(V\)):
\( V = V_{\text{ext}} - V_{\text{int}} \)
\( V = 4186,67 - 3053,63 \)
\( V \approx 1133,04 \, \text{cm}^3 \)
a)
Densidade da esfera (\(\rho\)):
\( \rho = \frac{m}{V} = \frac{1200}{1133,04} \)
\( \rho \approx 1,06 \, \text{g/cm}^3 \)
b) Massa específica do material (\(\mu\)):
A massa específica é a mesma que a densidade da esfera:
\( \mu \approx 1,06 \, \text{g/cm}^3 \)
Problema 4
Se as massas são iguais, então \(m_1 = m_2\) e cada um contribui com metade do volume total da mistura.
Massa específica da mistura (\(\mu_{\text{mistura}}\)):
\( \mu_{\text{mistura}} = \frac{\mu_1 + \mu_2}{2} \)
\( \mu_{\text{mistura}} = \frac{0,40 + 1,0}{2} \)
\( \mu_{\text{mistura}} = 0,70 \, \text{g/cm}^3 \)