Pressão Atmosférica e a Experiência de Torricelli
A atmosfera terrestre é composta por uma mistura de gases que exercem pressão sobre a superfície da Terra. Esta pressão, conhecida como pressão atmosférica, varia conforme a altitude. À medida que nos afastamos da superfície do planeta, o ar se torna progressivamente mais rarefeito, resultando em uma diminuição da pressão atmosférica.
O físico italiano Evangelista Torricelli (1608-1647) foi um discípulo de Galileu e é famoso por realizar a primeira medição da pressão atmosférica ao nível do mar. Sua experiência fundamental contribuiu significativamente para a compreensão da física atmosférica.
Torricelli utilizou um tubo de aproximadamente 1 metro de comprimento, completamente cheio de mercúrio (Hg) e com uma extremidade tampada. Em seguida, ele colocou o tubo de ponta-cabeça, com a extremidade aberta submersa em um recipiente também contendo mercúrio. Após destampar o tubo, o nível do mercúrio no tubo desceu até estabilizar-se em 76 centímetros, deixando um espaço vazio acima do mercúrio, conhecido como vácuo de Torricelli.
Essa experiência demonstrou que a pressão atmosférica ao nível do mar é capaz de sustentar uma coluna de mercúrio de 76 cm de altura. Esse valor se tornou uma referência para medições de pressão e contribuiu para o desenvolvimento do barômetro de mercúrio.
Torricelli observou que a pressão atmosférica equilibra o peso da coluna de mercúrio, concluindo que o peso do ar na atmosfera é o responsável por essa pressão.
Esse experimento não apenas comprovou a existência da pressão atmosférica, mas também abriu caminho para uma nova compreensão das forças atuantes na atmosfera terrestre. O trabalho de Torricelli é um marco na história da física e continua sendo uma base fundamental para estudos meteorológicos e de ciências atmosféricas.

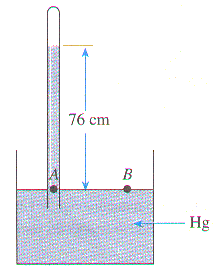
Na figura, as pressões nos pontos A e B são iguais (pontos na mesma horizontal e no mesmo líquido). A pressão no ponto A corresponde à pressão da coluna de mercúrio dentro do tubo, e a pressão no ponto B corresponde à pressão atmosférica ao nível do mar:
pB = pA
e
pATM = pcoluna(Hg)
Como a coluna de mercúrio que equlibra a pressã atmosférica é de 76 cm, dizemos que a pressão atmosférica ao nível do mar equivale à pressão de uma coluna de mercúrio de 76 cm. Lembrando que a pressão de uma coluna de líquido é dada por dgh (g = 9,8 m/s2), temos no SI :pATM @ 76cmHg = 760mmHg = 1,01x105 Pa
A maior pressão atmosférica é obtida ao nível do mar (altitude nula). Para qualquer outro ponto acima do nível do mar, a pressão atmosférica é menor. A tabela a seguir apresenta a variação da pressão atmosférica de acordo com a altitude.
| Altitude (m) | Pressão atmosférica (mmHg) |
|---|---|
| 0 | 760 |
| 200 | 742 |
| 400 | 724 |
| 600 | 707 |
| 800 | 690 |
| 1000 | 674 |
| 1200 | 658 |
| 1400 | 642 |
| 1600 | 627 |
| 1800 | 612 |
| 2000 | 598 |
| 3000 | 527 |
Os manômetros (medidores de pressão) utilizam a pressão atmosférica como referência, medindo a diferença entre a pressão do sistema e a pressão atmosférica. Tais pressões chamam-se pressões manométricas. A pressão manométrica de um sistema pode ser positiva ou negativa, dependendo de estar acima ou abaixo da pressão atmosférica. Quando o manômetro mede uma pressão manométrica negativa, ele é cjamado de manômetro de vácuo.

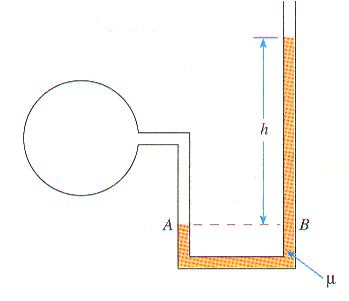
Pela diferença de níveis do líquido nos dois ramos do tubo em U, mede-se a pressão manométrica do sistema contido no reservatório. Escolhendo os dois pontos A e B mostrados na figura, temos:
\(p_{\text{A}} = p_{\text{B}}\)
\(p_{\text{Sistema}} = p_{\text{Atm}} + p_{\text{Líquido}}\)
\(p_{\text{Sistema}} = p_{\text{Atm}} + dgh\)
\(p_{\text{Manométrica}} = dgh\)
Exercícios
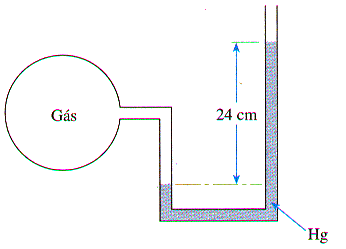
1. A figura representa um balão contendo gás, conectado a um tubo aberto com mercúrio. Se a pressão atmosférica local é a normal (76 cmHg), determine a pressão do gás, em cmHg.
2. Com base na figura, que representa um manômetro de tubo aberto, responda:
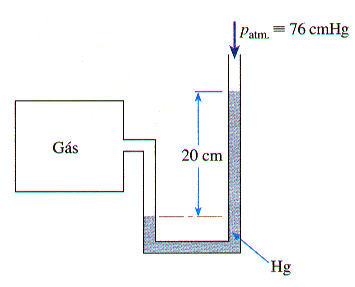
a) a quantos centímetros de Hg corresponde a pressão manométrica do gás ?
b) qual é a pressão manométrica do gás, em kPa ?
(Considere dHg = 13,6 g/cm3 )
Resoluções
Problema 1
Para determinar a pressão do gás no balão, utilizamos a pressão atmosférica local e a diferença de altura no tubo de mercúrio.
Dados:
Pressão atmosférica: \(76 \, \text{cmHg}\)
Diferença de altura: \(24 \, \text{cm}\)
A pressão do gás (\(P_{\text{gás}}\)) é calculada pela soma da pressão atmosférica (\(P_{\text{atm}}\)) com a diferença de altura (\(h\)):
\( P_{\text{gás}} = P_{\text{atm}} + h \)
Substituindo os valores fornecidos:
\( P_{\text{gás}} = 76 \, \text{cmHg} + 24 \, \text{cm} \)
\( P_{\text{gás}} = 100 \, \text{cmHg} \)
Portanto, a pressão do gás no balão é \(100 \, \text{cmHg}\).
Problema 2
a) Pressão manométrica do gás em cmHg
A diferença de altura entre os níveis de mercúrio nos dois braços do manômetro é de \(20 \, \text{cm}\). Como o mercúrio é deslocado pela pressão do gás, a pressão manométrica (\(P_{\text{man}}\)) do gás é igual a essa diferença de altura:
\( P_{\text{man}} = 20 \, \text{cmHg} \)
b) Pressão manométrica do gás em kPa
Para converter a pressão de cmHg para kPa, usamos a relação:
\( 1 \, \text{cmHg} = 133,322 \, \text{Pa} \)
Então,
\( P_{\text{man}} = 20 \, \text{cmHg} \times 133,322 \, \text{Pa/cmHg} \)
\( P_{\text{man}} = 2666,44 \, \text{Pa} \)
Convertendo para kPa (1 kPa = 1000 Pa):
\( P_{\text{man}} = \frac{2666,44 \, \text{Pa}}{1000} \)
\( P_{\text{man}} \approx 2,67 \, \text{kPa} \)
Portanto, a pressão manométrica do gás é \(2,67 \, \text{kPa}\).