Princípio de Arquimedes (EMPUXO)
Contam os livros que o sábio grego Arquimedes (282-212 AC) descobriu, enquanto tomava banho, que um corpo imerso na água se torna mais leve devido a uma força exercida pelo líquido sobre o corpo, vertical e para cima, que alivia o peso do corpo. Essa força, do líquido sobre o corpo, é denominada empuxo (\(E\)).
Portanto, num corpo que se encontra imerso em um líquido, agem duas forças: a força peso (\(P\)), devida à interação com o campo gravitacional terrestre, e a força de empuxo (\(E\)), devida à sua interação com o líquido.

Quando um corpo está totalmente imerso em um líquido, podemos ter as seguintes condições:
Para saber qual das três situações irá ocorrer, devemos enunciar o princípio de Arquimedes:
Todo corpo mergulhado num fluido (líquido ou gás) sofre, por parte do fluido, uma força vertical para cima, cuja intensidade é igual ao peso do fluido deslocado pelo corpo.
Seja \(V_f\) o volume de fluido deslocado pelo corpo. Então a massa do fluido deslocado é dada por:
\( m_f = \rho_f V_f \)
A intensidade do empuxo é igual à do peso dessa massa deslocada:
\( E = m_f g = \rho_f V_f g \)
Para corpos totalmente imersos, o volume de fluido deslocado é igual ao próprio volume do corpo. Neste caso, a intensidade do peso do corpo e do empuxo são dadas por:
\( P = \rho_c V_c g \quad \text{e} \quad E = \rho_f V_c g \)
Comparando-se as duas expressões observamos que:
Quando um corpo mais denso que um líquido é totalmente imerso nesse líquido, observamos que o valor do seu peso, dentro desse líquido, é aparentemente menor do que no ar. A diferença entre o valor do peso real e do peso aparente corresponde ao empuxo exercido pelo líquido:
\( P_{\text{aparente}} = P_{\text{real}} - E \)
Exemplo:
Um objeto com massa de 10 kg e volume de 0,002 m3 é colocado totalmente dentro da água (\((\rho=1 \text{kg/L})\).

(Use \( g = 10 \, \text{m/s}^2 \) .)
Resolução
Item a)
O valor do peso do objeto é dado por:
\( P = m \cdot g \)
Substituindo os valores:
\( P = 10 \, \text{kg} \cdot 10 \, \text{m/s}^2 \)
\( P = 100 \, \text{N} \)
Portanto, o peso do objeto é 100 N.
Item b)
A intensidade da força de empuxo que a água exerce no objeto é dada por:
\( E = \rho \cdot V \cdot g \)
Substituindo os valores:
\( E = 1000 \, \text{kg/m}^3 \cdot 0,002 \, \text{m}^3 \cdot 10 \, \text{m/s}^2 \)
\( E = 20 \, \text{N} \)
Portanto, a intensidade da força de empuxo é 20 N.
Item c)
O valor do peso aparente do objeto é dado por:
\( P_{\text{aparente}} = P - E \)
Substituindo os valores:
\( P_{\text{aparente}} = 100 \, \text{N} - 20 \, \text{N} \)
\( P_{\text{aparente}} = 80 \, \text{N} \)
Portanto, o peso aparente do objeto é 80 N.
Item d)
Para determinar a aceleração do objeto, usamos a segunda lei de Newton:
\( F_{\text{resultante}} = m \cdot a \)
A força resultante é a diferença entre o peso do objeto e a força de empuxo:
\( F_{\text{resultante}} = P - E \)
Substituindo os valores:
\( F_{\text{resultante}} = 100 \, \text{N} - 20 \, \text{N} \)
\( F_{\text{resultante}} = 80 \, \text{N} \)
Agora, podemos determinar a aceleração:
\( a = \frac{F_{\text{resultante}}}{m} \)
Substituindo os valores:
\( a = \frac{80 \, \text{N}}{10 \, \text{kg}} \)
\( a = 8 \, \text{m/s}^2 \)
Portanto, a aceleração do objeto é 8 m/s².
Flutuação
Princípio de Arquimedes (Empuxo)
Segundo os registros históricos, o sábio grego Arquimedes (282-212 AC) fez uma descoberta enquanto tomava banho: um corpo imerso na água aparenta ser mais leve devido a uma força exercida pelo líquido sobre o corpo, vertical e para cima, que alivia o peso do corpo. Essa força, do líquido sobre o corpo, é denominada empuxo (\(E\)).
Assim, em um corpo que se encontra imerso em um líquido, agem duas forças: a força peso (\(P\)), resultante da interação com o campo gravitacional terrestre, e a força de empuxo (\(E\)), causada pela interação com o líquido.
Quando um corpo está totalmente imerso em um líquido, podemos ter as seguintes condições:
Para determinar qual das três situações irá ocorrer, podemos enunciar o princípio de Arquimedes:
Todo corpo mergulhado em um fluido (líquido ou gás) sofre, por parte do fluido, uma força vertical para cima, cuja intensidade é igual ao peso do fluido deslocado pelo corpo.
Seja \(V_f\) o volume de fluido deslocado pelo corpo. Então a massa do fluido deslocado é dada por:
\( m_f = \rho_f V_f \)
A intensidade do empuxo é igual ao peso dessa massa deslocada:
\( E = m_f g = \rho_f V_f g \)
Para corpos totalmente imersos, o volume de fluido deslocado é igual ao próprio volume do corpo. Nesse caso, a intensidade do peso do corpo e do empuxo são dadas por:
\( P = \rho_c V_c g \quad \text{e} \quad E = \rho_f V_c g \)
Comparando-se as duas expressões, observamos que:
Quando um corpo mais denso que um líquido é totalmente imerso nesse líquido, observamos que o valor do seu peso, dentro desse líquido, é aparentemente menor do que no ar. A diferença entre o valor do peso real e do peso aparente corresponde ao empuxo exercido pelo líquido:
\( P_{\text{aparente}} = P_{\text{real}} - E \)
Para um corpo flutuando em um líquido, temos as condições a seguir.
1) Ele encontra-se em equilíbrio:
E = P
2) O volume de líquido que ele desloca é menor do que o seu volume:
Vdeslocado < Vcorpo
3) Sua densidade é menor do que a densidade do líquido:
dcorpo < dlíquido
4) O valor do peso aparente do corpo é nulo:
Paparente = P – E = O
A relação entre os volumes imerso e total do corpo é dada por:
E = P
dliquidoVimersog = dcorpoVcorpog
![]()
Exemplo:
Um bloco de madeira, \( \rho_c = 0,65 \, \text{g/cm}^3 \), com 20 cm de aresta, flutua na água \( \rho_c = 1,0 \, \text{g/cm}^3 \). Determine a altura do cubo que permanece dentro da água.
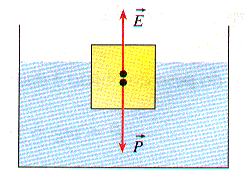
Resolução
Para resolver esse problema, usamos o princípio de Arquimedes, que afirma que a força de empuxo é igual ao peso do volume de fluido deslocado pelo corpo.
Primeiro, calculamos o volume do cubo de madeira:
\( V = a^3 = (20 \, \text{cm})^3 = 8000 \, \text{cm}^3 \)
Agora, calculamos a massa do cubo de madeira:
\( m = \rho_c \cdot V = 0,65 \, \text{g/cm}^3 \cdot 8000 \, \text{cm}^3 = 5200 \, \text{g} = 5,2 \, \text{kg} \)
A força peso do cubo de madeira é:
\( P = m \cdot g = 5,2 \, \text{kg} \cdot 10 \, \text{m/s}^2 = 52 \, \text{N} \)
Para o cubo flutuar, a força de empuxo deve ser igual à força peso. A força de empuxo é dada por:
\( E = \rho_{\text{água}} \cdot V_{\text{imerso}} \cdot g \)
Como \(E = P\), temos:
\( \rho_{\text{água}} \cdot V_{\text{imerso}} \cdot g = P \)
\( 1,0 \, \text{g/cm}^3 \cdot V_{\text{imerso}} \cdot 10 \, \text{m/s}^2 = 52 \, \text{N} \)
Convertendo \(1,0 \, \text{g/cm}^3\) para \(1,0 \, \text{kg/L}\) ou \(1000 \, \text{kg/m}^3\):
\( 1000 \, \text{kg/m}^3 \cdot V_{\text{imerso}} \cdot 10 \, \text{m/s}^2 = 52 \, \text{N} \)
\( V_{\text{imerso}} = \frac{52 \, \text{N}}{1000 \, \text{kg/m}^3 \cdot 10 \, \text{m/s}^2} = 0,0052 \, \text{m}^3 = 5200 \, \text{cm}^3 \)
O volume imerso do cubo de madeira é igual à altura imersa (\(h\)) vezes a área da base do cubo (\(a^2\)):
\( V_{\text{imerso}} = h \cdot a^2 \)
Portanto:
\( h \cdot (20 \, \text{cm})^2 = 5200 \, \text{cm}^3 \)
\( h \cdot 400 \, \text{cm}^2 = 5200 \, \text{cm}^3 \)
\( h = \frac{5200 \, \text{cm}^3}{400 \, \text{cm}^2} = 13 \, \text{cm} \)
Portanto, a altura do cubo que permanece dentro da água é \(13 \, \text{cm}\).
Exercícios
1. Um corpo está flutuando em um líquido. Nesse caso
(A) o empuxo é menor que o peso.
(B) o empuxo é maior que o peso.
(C) o empuxo é igual ao peso.
(D) a densidade do corpo é maior que a do líquido.
(E) a densidade do corpo é igual a do líquido
2.Uma esfera maciça e homogênea, de massa específica igual a \( 2,4 \, \text{g/cm}^3 \), flutua mantendo 20% do seu volume acima da superfície livre de um líquido. A massa específica desse líquido, em \( \text{g/cm}^3 \), é igual a:
(A) 4,8
(B) 3,2
(C) 2,0
(D) 1,6
(E) 1,2
3. Um ovo colocado num recipiente com água vai até o fundo, onde fica apoiado, conforme a figura . Adicionando-se sal em várias concentrações, ele assume as posições indicadas nas outras figuras B, C, D e E .

A situação que indica um empuxo menor do que o peso do ovo é a da figura
(A) A
(B) B
(C) C
(D) D
(E) E
4.Uma esfera maciça e homogênea, de massa específica igual a 2,4 g/cm3, flutua mantendo 20% do seu volume acima da superfície livre de um líquido. A massa específica desse líquido, em g/cm3 , é igual a
(A) 1,9
(B) 2,0
(C) 2,5
(D) 3,0
(E) 12,0
5. interior de um recipiente encontra-se um corpo em equilíbrio mergulhado num líquido de densidade 0,8 g/cm3, conforme a figura. Se este mesmo corpo for colocado em outro recipiente, contendo água ( densidade igual a 1g/cm3) podemos afirmar que
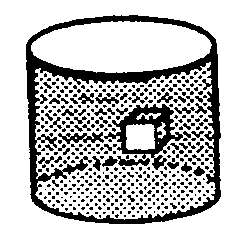
(A) o corpo irá afundar e exercer força no fundo do recipiente.
(B) o corpo continuará em equilíbrio, totalmente submerso.
(C) o corpo não flutuará.
(D) o corpo flutuará com mais da metade do volume submerso.
(E) o corpo flutuará com menos da metade do volume submerso
Problema 1
Quando um corpo está flutuando em um líquido, a força de empuxo que atua sobre ele é igual ao seu peso. Isso ocorre porque o corpo desloca uma quantidade de líquido cujo peso é igual ao seu próprio peso. Portanto, a resposta correta é:
\( \boxed{\text{(C)} \, \text{ o empuxo é igual ao peso}} \)
Problema 2
Vamos resolver este problema passo a passo.
Quando a pedra está submersa no líquido, a perda aparente de peso é igual ao empuxo (\(E\)) exercido pelo líquido. Sabemos que a perda aparente de peso é igual à metade do peso da pedra fora do líquido, ou seja:
\( E = \frac{P}{2} \)
A força de empuxo \(E\) é dada por:
\( E = \rho_{\text{líquido}} \cdot V \cdot g \)
E o peso \(P\) da pedra é dado por:
\( P = \rho_{\text{pedra}} \cdot V \cdot g \)
Como \(E = \frac{P}{2}\):
\( \rho_{\text{líquido}} \cdot V \cdot g = \frac{1}{2} \left( \rho_{\text{pedra}} \cdot V \cdot g \right) \)
Cancelando \(V\) e \(g\) de ambos os lados da equação, obtemos:
\( \rho_{\text{líquido}} = \frac{\rho_{\text{pedra}}}{2} \)
Substituindo os valores fornecidos:
\( \rho_{\text{líquido}} = \frac{3,2 \, \text{g/cm}^3}{2} = 1,6 \, \text{g/cm}^3 \)
Portanto, a resposta correta é:
\( \boxed{\text{(D)} \, 1,6 \, \text{g/cm}^3} \)
Problema 3
Vamos analisar cada figura:
Portanto, a situação que indica um empuxo menor do que o peso do ovo é:
\( \boxed{\text{A}} \)
Problema 4
Princípio de Arquimedes: Para um corpo flutuante, a força de empuxo é igual ao peso do corpo.
Força de Empuxo (\( E \)):
\( E = \rho_{\text{líquido}} \cdot V_{\text{imerso}} \cdot g \)
Onde:
Peso da Esfera (\( P \)):
\( P = \rho_{\text{esfera}} \cdot V_{\text{esfera}} \cdot g \)
Onde:
Equilíbrio: Como a esfera flutua, a força de empuxo é igual ao peso da esfera.
\( E = P \)
Volume Imerso: Dado que a esfera mantém 20% do seu volume acima da superfície, 80% do seu volume está submerso.
\( V_{\text{imerso}} = 0,8 \cdot V_{\text{esfera}} \)
Igualando as forças:
\( \rho_{\text{líquido}} \cdot (0,8 \cdot V_{\text{esfera}}) \cdot g = \rho_{\text{esfera}} \cdot V_{\text{esfera}} \cdot g \)
Simplificação: Cancelando \( V_{\text{esfera}} \) e \( g \) de ambos os lados da equação:
\( \rho_{\text{líquido}} \cdot 0,8 = 2,4 \)
Encontrando \(\rho_{\text{líquido}}\):
\( \rho_{\text{líquido}} = \frac{2,4}{0,8} \)
\( \rho_{\text{líquido}} = 3,0 \, \text{g/cm}^3 \)
Portanto, a massa específica do líquido é:
\( \boxed{(D)3,0 \, \text{g/cm}^3} \)
Problema 5
Densidade e Empuxo:
Densidade do Líquido Original: \( \rho_{\text{original}} = 0,8 \, \text{g/cm}^3 \)
Densidade da Água: \( \rho_{\text{água}} = 1,0 \, \text{g/cm}^3 \)
Situação Inicial
O corpo está em equilíbrio no líquido de densidade \(0,8 \, \text{g/cm}^3\), ou seja, o empuxo é igual ao peso do corpo.
\( E_{\text{original}} = P \)
Como o corpo está em equilíbrio, sabemos que a densidade do corpo (\( \rho_{\text{corpo}} \)) deve ser igual à densidade do líquido (\(0,8 \, \text{g/cm}^3\)).
Situação na Água
Quando o corpo é colocado em água (\( \rho_{\text{água}} = 1,0 \, \text{g/cm}^3\)), o empuxo é dado por:
\( E_{\text{água}} = \rho_{\text{água}} \cdot V_{\text{imerso}} \cdot g \)
Como a densidade da água é maior, o empuxo exercido pela água será maior do que o empuxo exercido pelo líquido original, para o mesmo volume submerso. Portanto, para que o corpo flutue em equilíbrio na água, ele deslocará menos volume de água do que no líquido original.
Isso significa que:
Para determinar se o corpo flutuará com mais ou menos da metade do volume submerso, comparamos as densidades. Como a densidade da água (\(1,0 \, \text{g/cm}^3\)) é maior que a densidade do corpo (\(0,8 \, \text{g/cm}^3\)), o corpo deslocará um volume de água correspondente a 80% do seu volume total, para que o empuxo iguale ao peso do corpo.
Portanto, a resposta correta é:
\( \text{(D)} \) o corpo flutuará com mais da metade do volume submerso.