
|
Cálculo de desempenho - Média harmônica |
Antes, leia: Média e desvio padrão de uma prova
1) Calcule o escore padronizado das 9 matérias, utilizando a fórmula:
Onde:
EP: escore padronizado na prova
EB: escore do candidato na prova (escore bruto em prova da UFRGS ou escore resultante do ENEM)
MD: média dos escores da prova
DP: desvio padrão da prova
2) Calcule a média harmônica:
AC: ARGUMENTO DE CLASSIFICAÇÃO
P: PESO DA PROVA (1, 2 ou 3)
A equação acima não leva em consideração o Benefício do ENEM. Para saber como funciona o cálculo da média harmônica com benefício do ENEM, clique aqui.
DICAS GERAIS
1) A média harmônica é um tipo de média que privilegia o desempenho harmônico do candidato. Terá melhor desempenho o candidato que tiver um desempenho médio em todas as provas, do que aquele que for muito bem numa e muito mal noutra. Exemplo:
| Aluno | Escore padronizado na prova 1 | Escore padronizado na prova 2 | Média harmônica das duas provas |
|---|---|---|---|
| João | 500 | 500 | 500 |
| Maria | 100 | 900 | 180 |
2) O desvio é a diferença entre o escore de cada aluno e a média. O DESVIO PADRÃO (DV) é a média destes desvios. Assim, numa prova que a média foi 12, calcula-se a diferença entre a nota de cada aluno e a média. Somam-se todos os desvios e divide-se pelos número de alunos. O desvio padrão sempre é divulgado, juntamente com a média, pela COPERSE.
3) Uma forma fácil de calcular o escore padronizado de uma prova é fazer o seguinte:
- se você acertar exatamente a média numa prova, seu escore padronizado será 500
- para cada desvio padrão que você obtiver, o seu EP aumenta em 100
Vejamos um exemplo onde a MÉDIA da prova foi 12 acertos e o DESVIO PADRÃO foi 4:
| Aluno | Número de acertos | Escore padronizado |
|---|---|---|
| João | 12 | 500 |
| Maria | 16 | 600 (1 desvio acima) |
| Pedro | 20 | 700 (2 desvios acima) |
| José | 8 | 400 (1 desvio abaixo) |
Comentários
1) Para cursos com argumento de classificação muito "baixos", em geral, basta o aluno não ser eliminado.2) As quantidades de acertos necessários são apenas uma referencial. Sugerimos uma margem de erro , em geral, de 10% para mais, como forma de "garantia".
3) A média de português que interessa é aquela calculada junto com a redação, levando-se em conta o desempenho (de 0 a 50) dos candidatos não eliminados.
4) Historicamente a média do último classificado não oscila em mais de 5% de um ano para outro.
Média e Desvio Padrão
O entendimento natural que grande parte dos candidatos utiliza para avaliar seus desempenhos nas provas é: "acertei mais ou menos questões do que a média?". Claro que a premissa vigente é a de que os candidatos mais bem preparados superam, em número de acertos, a média das provas.
0 resultado de uma prova, normalmente, é conhecido através de informações como média e desvio padrão, bem como pela distribuição de frequências do número de acertos dos candidatos, expressos em forma gráfica. Este gráfico, denominado histograma, mostra, no eixo dos X (abscissas), o número de questões e, no eixo dos Y, o número de candidatos que acertaram o referido número de questões. O que significam essas informações?
Numa distribuição de frequências, há três medidas importantes: a moda, a mediana e a média. A primeira é o "pico", isto é, o ponto no eixo das abscissas de maior frequência. A mediana é o ponto, no eixo das abscissas, que divide as ocorrências em duas frações iguais, cada uma com 50% das frequências. A média é o ponto, no eixo das abscissas, que faria com que o gráfico ficasse equilibrado, não inclinando nem para a esquerda nem para a direita; em suma, a média é o ponto, no eixo das abscissas, situado na vertical que passa pelo centro de gravidade da figura.
O que se deseja em uma prova do Concurso Vestibular é um histograma formando uma curva simétrica, distribuídos entre 0 e 25 acertos, concentrando moda, mediana e média próximas a 12,5 acertos, exibindo uma distribuição balanceada de acertos, tanto à esquerda como à direita do centro de distribuição, de acordo com o gráfico apresentado na figura a seguir.
O gráfico mostra uma distribuição normal rigorosamente simétrica. No centro da distribuição, coincidem média, mediana e moda. Uma curva de distribuição normal (ou Curva de Gauss) tem como característica englobar 99,73% das ocorrências no intervalo compreendido entre a média e ± 3 desvios padrão, conforme detalhado no mesmo gráfico.
O desvio padrão de uma prova mede o grau de dispersão dos candidatos em relação à média, isto é, o quanto o conjunto de candidatos se distanciou da média, tanto além como aquém do centro de distribuição. Isso significa que os escores obtidos por 99,73% dos candidatos estarão compreendidos entre a média e ± 3 desvios padrão, ou seja, salvo raras exceções, todos os candidatos estarão neste intervalo.
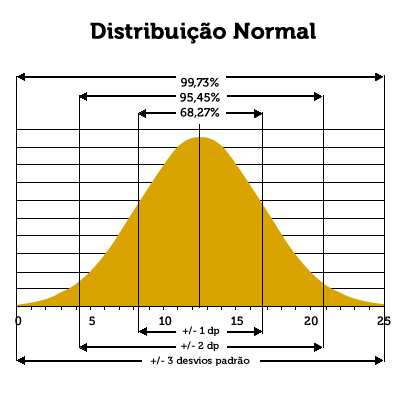
Ao se elaborar uma prova, espera-se que o resultado da aplicação da mesma gere uma "curva de distribuição normal", isto é, essa prova deve gerar uma média de 12,5 acertos e os candidatos devem estar distribuídos simetricamente entre zero e 25 acertos (ou entre dois limites internos desse intervalo, eqüidistantes de 12,5).
A obtenção de uma distribuição simétrica com 100% das ocorrências entre 0 e 25 acertos, em uma prova de 25 questões e média de 12,5 acertos, pode ser possível quando se obtém um desvio padrão de 4,166 acertos. Nesse caso, se o histograma assumir formato semelhante ao da curva normal, todos os escores possíveis de serem obtidos pelos candidatos ficariam simetricamente contidos no intervalo entre a média e ± 3 desvios padrão, ou seja, entre O acertos (12,5 - (3 x 4,166)) e 25 acertos (12,5 + (3 x 4,166)).
Infelizmente, não é fácil obter uma curva de distribuição normal. O resultado obtido pelos candidatos em uma prova depende de muitos fatores, entre os quais podem ser destacados a preparação dos mesmos e o grau de dificuldade da prova. Por isso mesmo, é importante poder avaliar uma prova através do resultado obtido na sua aplicação.
A informação da média permite verificar o grau de facilidade da prova para a população que a realizou. Quanto menor a média (abaixo de 12,5 acertos), menor a facilidade dos candidatos com as questões da mesma. Quanto maior a média (acima dos 12,5 acertos), maior a facilidade dos candidatos com as questões propostas.
Uma prova, com histograma normal, com média de 12,5 acertos e desvio padrão de 3,5 acertos significa que 99,73% dos candidatos serão encontrados entre os escores 3 e 22 acertos, (12,5 - (3 x 3,5)) e (12,5 + (3 x 3,5)). Isso significa que os candidatos com escores 0, 1, 2, 23, 24 e 25 acertos serão 0,23% da população, portanto pouquíssimos, conforme mostrado na figura a seguir correspondente à distribuição com desvio 3,5.
Enquanto que numa prova, também com histograma normal, com média de 12,5 acertos, mas desvio padrão de 1,5 acertos significa que 99,73% dos candidatos serão encontrados entre os escores 8 e 17 acertos, (12,5 - (3 x 1,5)) e (12,5 + (3 x 1,5)). Isto é, também haverá poucos candidatos (0,23%) com escores de 0 até 7 e de 18 até 25 acertos, conforme mostrado na figura correspondente à distribuição com desvio 1,5.
Analisando as duas figuras, que seguem, é possível concluir que, quanto maior for o desvio padrão, mais aberta é a curva (maior dispersão), ou seja, maior variedade de escores obtidos pelos candidatos e melhores condições de discriminar a qualificação dos candidatos. Curvas muito fechadas (pequeno desvio padrão) significam menor dispersão, ou seja, grande concentração de escores e menor variedade dos mesmos (muitos empates). Em outras palavras, se houver muitos empates, a prova poderá não avaliar devidamente a preparação dos candidatos. Ao mesmo tempo, provas muito difíceis não diferenciam escores obtidos unicamente através de acerto casual.
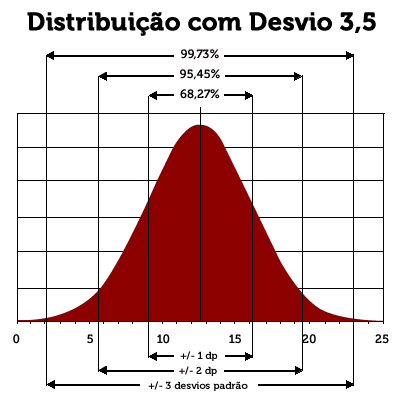
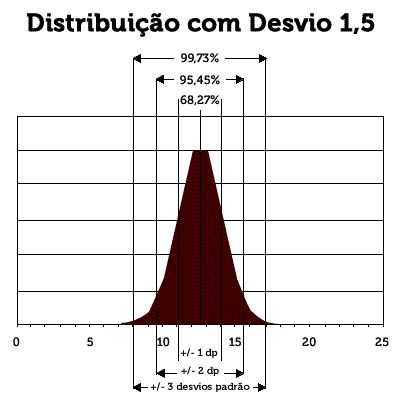
As informações de média e desvio padrão combinadas permitem uma análise muito interessante da prova.
Curva estreita e bem para a esquerda significa prova muito difícil (média muito abaixo de 12,5 acertos e concentrada em poucos escores). Curva estreita e bem para a direita significa prova muito fácil (média muito acima de 12,5 acertos e concentrada em poucos escores).
Daí conclui-se que o desvio padrão, em conjunto com a média da prova, permite identificar:
- o grau de complexidade da prova;
- a aptidão da prova para discriminar a preparação dos candidatos (qualidade das questões).
Provas Comentadas - Processo de Avaliação
Publicado pela COPERSE - UFRGS
Dúvidas?
Prof. Alberto Ricardo Präss
E-mail: albertoprass@gmail.com
 DICAS
DICAS
Dicas de Estudo, dicas em vídeo, planejamento de estudos, ...  PROVAS
PROVAS
As provas, gabaritos e resoluções dos últimos vestibulares.
 ESTATÍSTICAS
ESTATÍSTICAS
Confira as médias, desvios, argumentos, densidades e outros dados dos vestibulares anteriores.
 PROGNÓSTICOS
PROGNÓSTICOS
Calcule seu desempenho e estime quantos acertos serão necessários para ser aprovado.