Índice
Passemos agora a uma importante consequencia da teoria da relatividade, que desempenha um papel essencial na física nuclear e na física das partículas elementares. Falaremos sobre a relação universal entre a energia e a massa.
A relação entre a energia e a massa resulta da lei da conservação da energia e do fato de a massa do corpo depender da velocidade do movimento. Isto pode ser observado no seguinte exemplo simples. Quando se aquece um gás num recipiente é-lhe transmitida uma determinada energia. A velocidade do movimento calorífico caótico das moléculas depende da temperatura e aumenta com o aquecimento do gás. O aumento da velocidade do movimento das moléculas, de acordo com a fórmula (6) , significa o aumento da massa de todas as moléculas. Consequentemente, a massa do gás no recipiente aumenta quando aumenta a sua energia interna. Entre a massa do gás e a sua energia existe uma relação. <
A relação entre a massa e a energia no caso de um movimento lento. É mais simples estabelecer a relação entre a massa e a energia no exemplo do movimento de um corpo com velocidade v , bastante menor do que a velocidade da luz c . Para isso, deduzamos a expressão aproximada da dependência da massa em relação à velocidade quando v << c . O denominador na fórmula ( 6) escreve-se sob a forma.
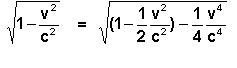
Desprezando a grandeza
![]()
obtemos:
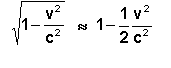
Por isso
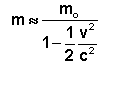
Multiplicando o numerador e o denominador por ![]() e desprezando de novo o membro
e desprezando de novo o membro![]() , obtemos a seguinte fórmula aproximada:
, obtemos a seguinte fórmula aproximada:
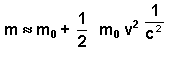
Daqui resulta que a variação da massa do corpo![]() , quando aumenta a sua energia cinética em
, quando aumenta a sua energia cinética em
![]()
exprime-se assim
![]()
Isto significa que o incremento da massa do corpo quando aumenta a sua velocidade, é igual à energia cinética que lhe é transmitida, dividida pelo quadrado da velocidade da luz.
A fórmula de Einstein. Na teoria da relatividade, este resultado é amplamente generalizado. Com o auxílio desta teoria, Einstein estabeleceu a relação geral entre a energia e a massa, que é dada por uma fórmula muito simples:
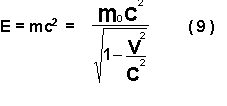
A energia dum corpo ou dum sistema de corpos é igual à massa multiplicada pelo quadrado da velocidade da luz. Em toda a física só se encontram duas ou três fórmulas universais tão simples como esta que relacionam as grandezas físicas fundamentais.
Se a energia do sistema varia, então varia também a sua massa:
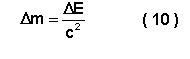
Visto que o coeficiente ![]() é muito pequeno, para que se note a variação da massa é
necessário que haja grandes mudanças de energia. Quando se dão reações químicas ou
quando se aquece um corpo em condições habituais, a variação da energia é tão
pequena que variação correspondente da massa não pode ser verificada experimentalmente.
Uma chaleira quente tem a massa maior do que uma fria; mas nem com o auxílio de balanças
muito sensíveis seria possível medir a diferença. Só quando se transforma o núcleo
atômico e as partículas elementares é que a variação de energia é tão grande que a
alteração da massa nessa altura já pode ser verificada.
é muito pequeno, para que se note a variação da massa é
necessário que haja grandes mudanças de energia. Quando se dão reações químicas ou
quando se aquece um corpo em condições habituais, a variação da energia é tão
pequena que variação correspondente da massa não pode ser verificada experimentalmente.
Uma chaleira quente tem a massa maior do que uma fria; mas nem com o auxílio de balanças
muito sensíveis seria possível medir a diferença. Só quando se transforma o núcleo
atômico e as partículas elementares é que a variação de energia é tão grande que a
alteração da massa nessa altura já pode ser verificada.
Quando explode uma bomba de hidrogênio liberta-se uma grande quantidade de energia - certa de 1017 J. Esta energia é superior à produção de energia elétrica em toda a Terra durante vários dias. A energia é transportada com a radiação. A radiação, além da energia, tem massa, que é aproximadamente igual a 0,1% da massa dos materiais iniciais.
Energia de repouso. Quando a velocidade do movimento de um corpo é reduzida ( v << c) , então a fórmula ( 9 ) pode escrever-se sob a forma 1 ) :
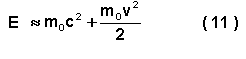
Neste caso, o segundo termo é a energia cinética habitual do corpo. Maior interesse desperta o primeiro membro : ele define a energia do corpo quando a velocidade é igual a zero ¾ a chamada energia de repouso E 0 :
![]()
Este resultado merece atenção. Qualquer corpo, pelo simples fato de existir, tem uma energia que é proporcional à massa de repouso m0 .
Quando se transformam partículas elementares com massa de repouso diferente de zero, em partículas com m0 = 0 , a energia de repouso das primeiras é transmitida às segundas totalmente sob a forma de energia cinética.
Este fato é a demonstração experimental mais evidente da existência de energia de repouso.
Textos Complementares