O motivo da inconsistência das noções clássicas de espaço e de tempo é a suposição errada sobre a possibilidade de transmissão instantânea de interação e de sinais de um ponto do espaço para outro. A existência de um limite finito da velocidade de transmissão de interação torna necessária uma mudança profunda das opções habituais de espaço e de tempo, baseadas na experiência quotidiana. O conceito de tempo absoluto, que decorre a um ritmo estabelecido de uma vez para sempre, independentemente da matéria e do tempo, revelou-se incorreto.
Se admitirmos que os sinais se propagam instantaneamente, então a afirmação de que os acontecimentos em dois pontos A e B, separados no espaço, ocorreram simultaneamente terá um significado absoluto. É possível colocar nos pontos A e B relógios e sincronizá-los por meio de sinais instantâneos. Se um sinal desses saiu de A, por exemplo, às 0h45m e, nesse mesmo instante, chegou ao ponto B, de acordo com o relógio neste ponto, então só dois relógios indicam a mesma hora, ou seja, estão sincronizados. Se não se dá tal coincidência, podem sincronizar-se os relógios, adiantando aquele que indica menos horas no momento da emissão do sinal.
Quaisquer acontecimentos, por exemplo, dois relâmpagos, são simultâneos se ocorrerem quando os relógios sincronizados indiquem a mesma hora.
Só colocando nos pontos A e B relógios sincronizados se pode ajuizar se quaisquer dois acontecimentos nestes pontos se dão ao mesmo tempo ou não. Mas como é que podemos sincronizar relógios que se encontram a uma dada distância um do outro, se a velocidade de propagação dos sinais não é infinitamente grande?
Para sincronizar os relógios é natural recorrer a sinais luminosos ou outros sinais eletromagnéticos, visto que a velocidade das ondas eletromagnéticas no vácuo é uma grandeza constante, conhecida com exatidão.
É este o método utilizado para verificar as horas pelo rádio. Os sinais de tempo ajudam a sincronizar os nossos relógios com os relógios-padrão exatos. Sabendo a distância entre a estação de rádio e a nossa casa pode-se calcular a correção correspondente ao atraso do sinal. Esta correção, é claro, é muito pequena. Na nossa vida quotidiana ela não tem qualquer significado. Mas no caso das grandes distâncias cósmicas ela pode tornar-se muito importante.
Vejamos detalhadamente um método simples de sincronização de relógios que não exige nenhum cálculo. Suponhamos que um astronauta quer saber se os relógios A e B colocados nos extremos opostos de uma nave espacial (fig. 2), estão certos entre si. Para isso, com o auxílio de um emissor, parado em relação à nave e colocado no meio dela, o astronauta produziu uma fulguração. A luz atinge ao mesmo tempo ambos os relógios. Se ambos eles marcarem a mesma hora, isso significa que estão sincronizados.
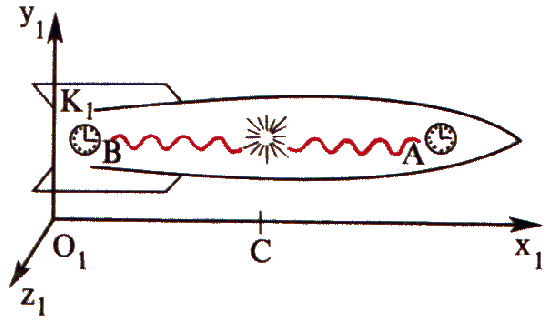
Fig. 2
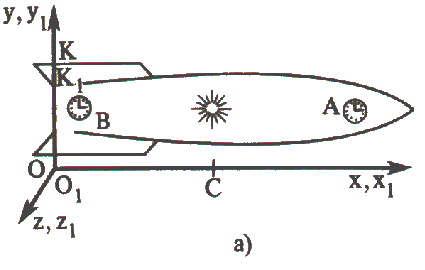
Mas só será assim em relação ao sistema de referência \( \textrm{K}_{1} \), ligado à nave. No sistema de referência \( \textrm{K} \), em relação ao qual a nave se move, a situação é diferente. O relógio que se encontra na parte da frente da nave afasta-se do lugar onde se encontra o emissor e, para atingir o relógio A, a luz tem de percorrer uma distância maior do que metade do comprimento da nave (fig. 3a, b), pelo contrário, o relógio B aproxima-se do emissor e o caminho percorrido pelo sinal luminoso é menor do que metade do comprimento da nave. Por isso, o observador no sistema \( \textrm{K} \) concluiu que os sinais não atingem ambos os relógios simultaneamente.
 |
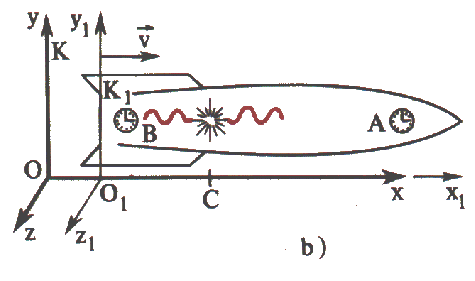 |
Fig. 3
Dois acontecimentos nos pontos A e B dão-se ao mesmo tempo no sistema \( \textrm{K}_{1} \) e em instantes diferentes no sistema \( \textrm{K} \). Mas de acordo com o princípio da relatividade os sistemas \( \textrm{K}_{1} \) e \( \textrm{K} \) são equivalentes. A nenhum destes sistemas se pode dar preferência. Por isso, somos obrigados a concluir que a simultaneidade dos acontecimentos em pontos distintos do espaço é relativa. O motivo do caráter relativo da simultaneidade é, como nós vimos, o valor finito da velocidade de propagação dos sinais.
É devido ao caráter relativo da simultaneidade que se explica o paradoxo dos sinais luminosos esféricos, sobre o qual se falou anteriormente. A luz atinge simultaneamente os pontos da superfície esférica com centro no ponto \( \textrm{O} \), do ponto de vista do observador que se encontra parado em relação ao sistema \( \textrm{K} \). Do ponto de vista do observador, ligado ao sistema \( \textrm{K}_{1} \), a luz atinge estes pontos em instantes diferentes.
Evidentemente, é verdadeiro o inverso: no sistema \( \textrm{K} \) a luz atinge os pontos da superfície esférica com centro em \( \textrm{O}_{1} \) em instantes diferentes, e não ao mesmo tempo, como parece ao observador que se encontra no sistema \( \textrm{K}_{1} \).
Daqui resulta que na realidade não existe nenhum paradoxo.
Índice
Textos Complementares